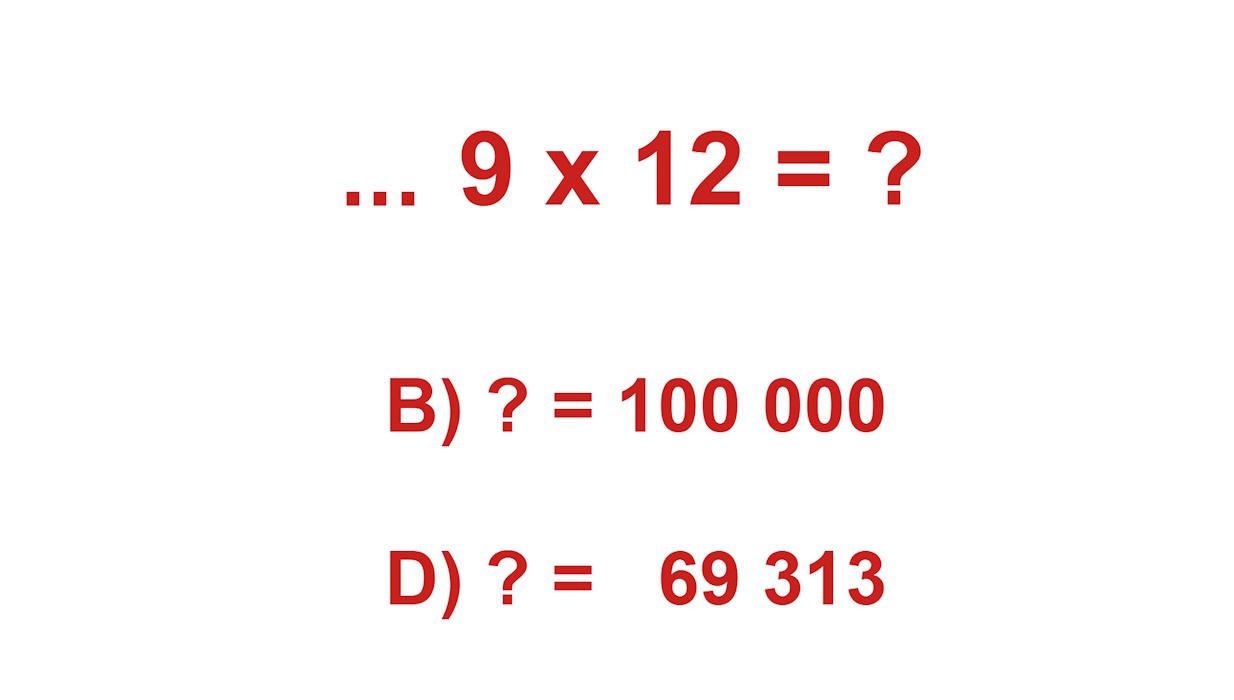Agykarbantartó matek: rájön 30 másodperc alatt, hogy melyik a helyes végeredmény? Csak fejben számolhat!
Tartsa karban a szellemi frissességét a matek segítségével! Itt egy jó kis agykarbantartó tesztfeladat – próbálja ki, megy-e számológép nélkül!
Nem csak a testünket kell rendszeresen gyakorolni, hanem az agyunk is folyamatos edzésre szorul, és mi sem jobb erre, mint egy kis matek. Ez a tantárgy sokak szerint kicsit száraz tud lenni, de mi próbálunk erre a vélekedésre hétről hétre rácáfolni. Például rögtön már attól izgalmasabb tud lenni ez a feladat, ha időre csinálja: ezúttal 20 másodpercre lőttük be a szintidőt, szóval ha van kedve kipróbálni, hogy megy-e ez a feladvány ilyen rövid idő alatt, indítsa be az órát, és azután görgessen lejjebb a teljes feladványhoz!
Agykarbantartó matek: melyik a helyes végeredmény?
Alább találja a teljes feladványt. Melyik a helyes végeredmény?
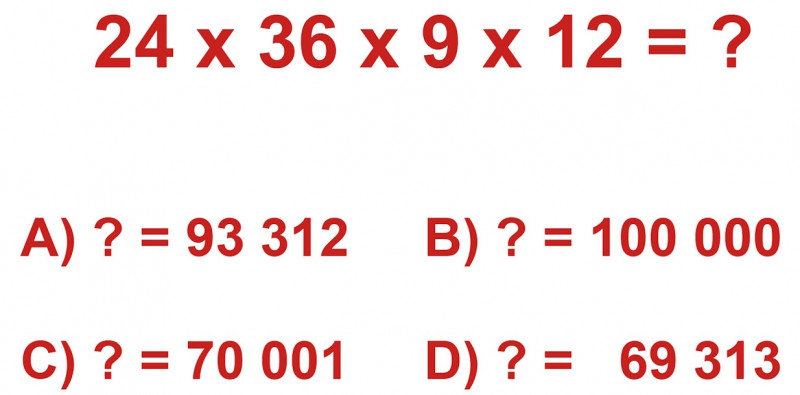
Ábra: 168.hu/Gyulai Bence
Mielőtt elkedvetlenedne, bátorítjuk önt: nem olyan nehéz ez a feladat, mint amilyennek elsőre valószínűleg tűnik! Ne adja fel egykönnyen, ön tud mindent, amit a megoldáshoz tudni kell, nem kell zseninek lenni ahhoz, hogy az ember eltalálja!
A megoldást az oldal alján találja
Ezek a cikkek is hasonló témákról szólnak
Szórakozás
2025. április 19., 14:55
Hogy megy a földrajz? Ez a műveltségi teszt segít ellenőrizni, hogy helyesen emlékszik-e még Európa fővárosaira.
Szórakozás
2025. április 15., 15:32
Húsvét alkalmából készített ma képrejtvényt a világhírű magyar grafikus, Dudolf.
Szórakozás
2025. április 16., 14:47
Figyelem, ezúttal a gyufás rejtvény nem áthelyezést, hanem csak elvételt tesz lehetővé!
Még egy utolsó esélyt adunk itt a lefelé görgetőknek egy random zenei videóval a visszaforduláshoz. Ha nem biztos a tippjében vagy esetleg nincs is tippje, még visszafordulhat! A klip alatt viszont már következik a helyes megfejtés.
Itt a megfejtés
Ha önnek sikerült ezt a négy számot tényleg fejben összeszoroznia, akkor gratulálunk, valószínűleg jelentkezhet valamilyen tévéműsorba, mert minden bizonnyal rendkívüli képességekkel rendelkezik.
De abban reménykedünk, hogy a többség akként gondolkodva jut el a helyes megoldásig, hogy nyilván nem adunk fel egy ilyen brutál fejszámolási feladatot, ezért csak van valami kerülőút, valami trükk, ahogy ki lehet számolni a négy szám szorzatát. Vagy ha azt nem, akkor esetleg azt, hogy melyik szám NEM lehet a négy megadott lehetőség közül a szorzat.
Egy egyszerű dolgot kellett észrevenni a feladványban, és innentől kezdve már rendkívül szimplává válik a feladat. Azt méghozzá, hogy a négy összeadandó szám mind a háromnak valamilyen többszöröse. A szorzat tehát nyilván szintén osztható lesz hárommal.
Ha ez a felismerés megvolt, akkor arra kellett még emlékezni a matekórákról, hogy miről lehet könnyen felismerni a hárommal osztható számokat: arról, hogy a számjegyeik összege is osztható hárommal. A B)-nél a számjegyek összege ugye egy, a százezer nem osztható hárommal, ezt a legkönnyebb kizárni. A C)-nél szintén egy pillantással megállapítható, hogy a javasolt végeredmény számjegyeinek összege 8, ez sem egy hárommal osztható szám, következésképpen nem lehet a végeredmény. A D) jelű válaszlehetőségnél feltüntetett szám négy hárommal osztható számból áll, plusz egy egyesből, tehát szintén nem lehet hárommal osztható – a számjegyeinek összege 22.
Az első végeredménynél viszont a számjegyek összege 21, ez tehát a négy lehetőség közül az egyetlen, amelyik osztható hárommal. A helyes megoldás tehát:
A) ? = 93 312
(Kiemelt kép: 168.hu/Gyulai Bence)
