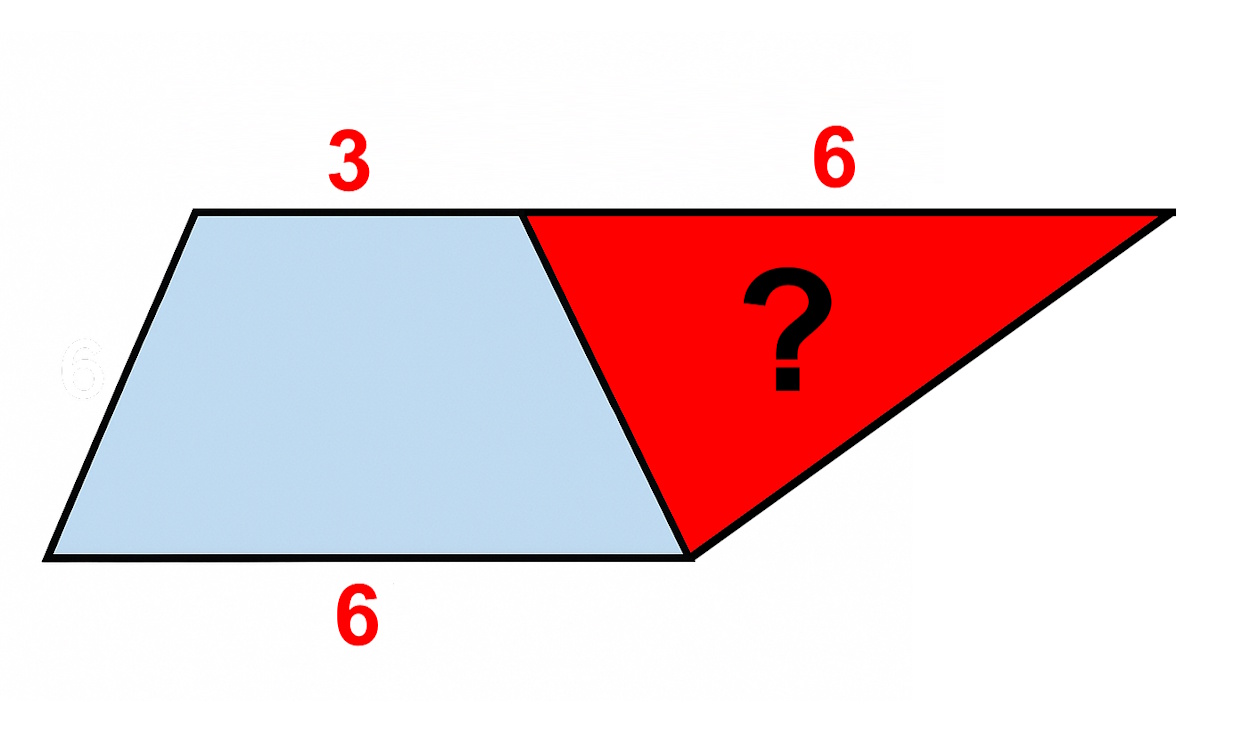
Agykarbantartó matek, villámgyors geometria: meg tudja mondani 1 perc alatt, mekkora a piros háromszög területe?
Jöjjön egy kis matek, jöjjön egy gyors geometria-feladat, aminek megoldásához csak általános iskolai ismeretek szükségesek!
A matek az egyik legjobb agykarbantartó, és bár van, aki nem annyira szereti, nekik is érdemes néha feleleveníteni legalább az általános iskolai ismereteket. Erre csodásan alkalmas az alábbi feladat, amit – vigyázat! – teljes egészében csak alább mutatunk, mert a fenti ábra nem tartalmaz minden adatot. De ahogy szoktuk, előbb jöjjön a visszaszámláló azok kedvéért, akik szeretnek az óra ellen játszani. Most a szintidő 60 másodperc! Elég lesz? Indítsa be a videót, jelzi majd, ha lejárt az idő. A teljes rejtvényt a visszaszámláló alatt találja.
Agykarbantartó matek: mekkora a piros háromszög területe?
A feladathoz azt kell még tudni a kékkel jelölt négyszögről, hogy az egy trapéz és hogy a területe 18. Így már meg tudja mondani, hogy mekkora a piros háromszög területe?
Ezek a cikkek is hasonló témákról szólnak
Szórakozás
2025. július 1., 14:42
Az irodalom a témája a mai rejtvénynek, illetve az alábbi két, tízes listának. De van egy kis kavarodás... Ön rendet tud vágni a címek között?
Szórakozás
2025. június 30., 16:34
Szarvashibának számít a helyesírás terén, ha az ember elrontja egy j/ly-t. Most azonban három olyan szót keresünk, amelyik j-vel és ly-nal egyaránt helyes.
Szórakozás
2025. június 26., 12:49
Európai országok legnagyobb városainak listáit mutatjuk, de a harmadik mindig hiányzik. Ha önnek jól megy a földrajz, biztosan kitalálja!
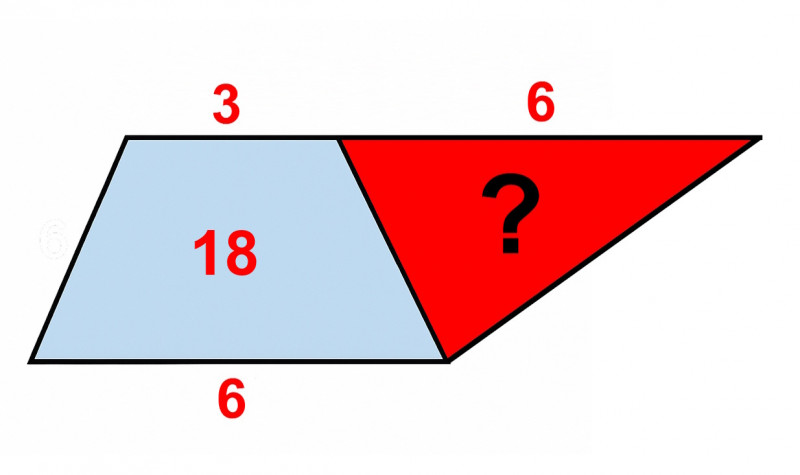
Ábra: 168.hu/Gyulai Bence
A megoldást az oldal alján találja
Egy random nemzenei videó következik most, de természetesen csak azért, hogy legyen min átgörgetni – ezzel próbáljuk biztosítani, hogy ne legyen egymáshoz túl közel a feladvány és megfejtése, illetve azt, hogy nehogy valaki véletlenül idejekorán meglássa a megoldást. Bár akinek van kedve egy kis irodalomhoz itt a nagy matekozás kellős közepén, annak igencsak ajánlom, hogy tekintse meg, hallgassa meg a felvételt!
Itt a megoldás
Bajban voltak azok ennél a feladatnál, akik nem emlékeznek, hogy hogyan kell kiszámolni a trapéz területét. Nos, ennek a négyszögnek a területe a következőképpen számolható: vesszük két párhuzamos oldalának összegét, azt elosztjuk kettővel és megszorozzuk a magassággal. A párhuzamos oldalak hosszát tudjuk, a magasságot nem, de a területet igen, és ez azért pont jó, mert a háromszögnek ugyanannyi a magassága, mint a trapéznak, tehát szükségünk lesz erre az adatra.
Szóval a kékkel jelölt trapéz két párhuzamos oldalának összege 6+3=9. Ha ezt elosztjuk kettővel, akkor 4,5 jön ki. Ezt a számot kell megszorozni a magassággal, hogy a trapéz területét kapjuk meg, azaz 4,5×m=18. Vagyis m=18÷4,5=4. A trapéz területe tehát csak akkor lehet 18, ha a trapéz magassága 4.
Így már meg is van a másik kulcsfontosságú adat a háromszög területének kiszámításához, hiszen itt a képlet az, hogy az alap hossza szorozva a magassággal, de osztva kettővel. Az alap ugye 6, a magasságot most számoltuk ki, hogy 4, tehát a piros háromszög területe 6×4÷2=24÷2=...
12!
(Kiemelt kép: 168.hu/Gyulai Bence)
